Data Envelopment Analysis
Within couple of days I have been testing DEA modelling (Data Envelopment Analysis) with different R-package. Finally,…. I have found such a comprehensive way to calculate Malmquist indices.

My primary purpose is to show how to use nonparametric methods for measuring efficiency and productivity by using R-programs nonparaeff -package.
At this same time I will show you how to present Malmquist indices within googleVis -world map and finally I will introduse how to make forecast chart for productivity (Chart 1), effectiveness and technical effectiveness indices. In this work I used R-program forecast -library.
Used R-library documentation:
nonparaeff
googleVis
forecast
First of all I would like to thank Author Dong-hyun Oh for nice work with this nonparaeff-package.
In this working paper I will use example of faremalm2. Like nonpraeff -package documentation we calculate Malmquist productivity growth index of OECD countries
(productivity, technical efficiency and efficiency). As data source we have used Penn World Table (like original sources) with following version:
OECD Timeseries 1980-1990 version pwt5.6
OECD Timeseries 1990-2009 version pwt7.0
In pwt7.0 I cannot find capital stock data, so I downloaded it from here (http://www.ifw-kiel.de/forschung/datenbanken/netcap)
Productivity calculation 1980-1990 As output variables is used Total GDP of a country. This variables is calculated using GDP per capita (rgdpl)
and amount of total population (pop). As input variables is used Total labor force (gdp/rgdpwok) and Total capital stock (kapw * labor)
In second productivity computing calculation 1990-2009 I only use one input and one output variables (labor and gdp). This is because there is no
capital stock data available in pwt7.0 (please correct this If I missed something). I will re-calculate this period asap when I get capital data from all countries.
In third productivity computing 1992-2002 I use pwt7.0 and get capital stock data from different OECD datasource
(http://www.ifw-kiel.de/forschung/datenbanken/netcap). As input I used labor and capital variables and as output variables gdp.
When use faremalm2 function you will get the following outputs:
pc.c –> Productivity growth for each country
pc.y –> A trend of productivity growth of SELECTED countries (in this work we use OECD)
tc.c –> Technical efficiency for each country
tc.y –> A trend of technical efficiency growth of SELECTED countries
ec.c –> Efficiency change for each country
ec.y –> A trend of efficiency change of SELECTED countries
Useage of faremalm2
faremalm2(dat = NULL, noutput = 1, id = “id”, year = “year”)
dat –> The format of this data frame is data.frame(id, year, outputs, inputs).
noutput –> number of outputs
id –> column name for DMU:s
year –> column name for the time index
## Malmquist productivity growth index of OECD countries
#First install data from OECD
install.packages("pwt") # (installing a package can take a couple of minutes)
#Setting the library into use
library(pwt) ## Use Penn World Table
library(nonparaeff) # DEA modelling
More information about pwt data you can find there (http://pwt.econ.upenn.edu/php_site/pwt_index.php)
#my.dat <- pwt5.6 #used in 1980-1990
#my.dat <- pwt6.3 #
my.dat <- pwt7.0 #used in 1990-2009 and 1992-2002
#head(my.dat)
summary(my.dat)
#my.dat$country
#capital stock data missing so we get it from there
# http://www.ifw-kiel.de/forschung/datenbanken/netcap
#picking up OECD countries
my.oecd.ctry <- c("AUS", "AUT", "BEL", "CAN", "CHE", "DNK", "ESP", "FIN", "FRA", "GBR", "GER", "GRC", "IRL", "ISL", "ITA", "JPN", "KOR", "LUX", "MEX", "NLD", "NOR", "NZL", "PRT", "SWE", "TUR", "USA", "DEU")
#NOTE WPCODE USED IN OLDER DATASET
#adding country code
#my.dat <- my.dat[my.dat$wbcode %in% my.oecd.ctry,] #use this with pwt5.6
my.dat <- my.dat[my.dat$isocode %in% my.oecd.ctry,] #use this with pwt7.0
summary(my.dat)
#selecting appropriate years
#my.dat <- my.dat[my.dat$year %in% 1980:1990,]
#my.dat <- my.dat[my.dat$year %in% 1950:1992,]
my.dat <- my.dat[my.dat$year %in% 1990:2009,]
#my.dat <- my.dat[my.dat$year %in% 1992:2002,]
summary(my.dat)
my.dat
Note! I encounter problem (NA or other reason) thats why I do this out of box. my.dat is transformed into data.frame and after
that modified with Excel. This is only used in timeseries 1992-2002 productivity calculation.
#uploading my.dat
#my.dat_df <- as.data.frame(my.dat)
#out
#write.table(my.dat_df, file = "c:/data/my.dat_df.txt", sep = "\t", col.names = NA, qmethod = "double")
Capital stock data inserted in this phase. source: http://www.ifw-kiel.de/forschung/datenbanken/netcap
#...and in both source
my.dat <- read.table(".../mydat1990_2009.csv", header=TRUE,
sep=";", na.strings="NA", dec=",", strip.white=TRUE)
my.dat <- read.table("http://ekqvist.goeuropeinfo.com/rbloggerqvist/
data/oecd/mydat1990_2009.csv", header=TRUE, sep=";", na.strings="NA",
dec=",", strip.white=TRUE)
#INSERTING some variables to my.dat (ie. INPUT and OUTPUT -variables calculation)
my.dat$rgdpl <- as.numeric(my.dat$rgdpl) ## GDP per capita
my.dat$pop <- as.numeric(my.dat$pop) ## total population (1000)
my.dat$rgdpwok <- as.numeric(my.dat$rgdpwok) ## GDP per labor
my.dat$gdp <- my.dat$rgdpl * my.dat$pop ## Total GDP of a country
my.dat$labor <- with(my.dat, gdp/rgdpwok) ## Total labor force
my.dat$capital <- with(my.dat, kapw * labor) ## Total capital stock MISSING pwt7 note: this is used in pwt5.6 #my.dat$capital <- as.numeric(my.dat$capital) ## Total capital stock ADDED FROM DIFF. SOURCE now used in time series 1993-2002
my.dat$kapw <- as.numeric(my.dat$kapw) ## Capital stock per labor MISSING pwt7 note: this is used in pwt5.6 #my.dat$kapw <- with(my.dat, my.dat$capital/my.dat$labor) ## Capital stock per labor now used in time series 1993-2002
#variable used in 1990-2009 Malmquist productivity calculation
#1980-1990
#1990-2009
#1992-2002
#these variables used in timeseries 1980-1990 and 1992-2002
#oecd <- my.dat[, c("country", "wbcode", "year", "gdp", "labor", "capital")] #used in time series 1980-1990
oecd <- my.dat[, c("country", "isocode", "year", "gdp", "labor")] # 1990-2009
#oecd <- my.dat[, c("country", "isocode", "year", "gdp", "labor", "capital")] #used in time series 1992-2002
summary(oecd)
head(oecd)
#removing NA-rows
oecd <- oecd[!is.na(oecd$capital),]
summary(oecd)
#Now calcuatel productivity (pc), effiency (ec) and technical efficiency (tc)
#huom. tämä on tehty eri aikasarjoille ja hyvä niin koska mahdollistaa eri aikajaksojen tarkastelun
library(nonparaeff) # DEA modelling
re.oecd <- faremalm2(dat = oecd, noutput = 1, id = "isocode", year = "year")
#re.oecd <- faremalm2(dat = oecd, noutput = 1, id = "wbcode", year = "year")
summary(re.oecd)
######################################################
#ISOCODE USED IN #1990-2009 and 1992-2002
#note:
## productivity growth for each country
pc.c <- tapply(re.oecd$pc, re.oecd$isocode, geometric.mean)
#pc.c <- tapply(re.oecd$pc, re.oecd$wbcode, geometric.mean)
## a trend of productivity growth of SELECTED countries
pc.y <- tapply(re.oecd$pc, re.oecd$year, geometric.mean)
## technical efficiency for each country
tc.c <- tapply(re.oecd$tc, re.oecd$isocode, geometric.mean)
#tc.c <- tapply(re.oecd$tc, re.oecd$wbcode, geometric.mean)
## a trend of technical efficiency growth of SELECTED countries
tc.y <- tapply(re.oecd$tc, re.oecd$year, geometric.mean)
## efficiency change for each country
ec.c <- tapply(re.oecd$ec, re.oecd$isocode, geometric.mean)
#ec.c <- tapply(re.oecd$ec, re.oecd$wbcode, geometric.mean)
## a trend of efficiency change of SELECTED countries
ec.y <- tapply(re.oecd$ec, re.oecd$year, geometric.mean)
######################################################
pc.c
#1980-1990, 1990-2009
#country -variable(we use it in google vis plotting)
## productivity growth for each country
pc.c <- tapply(re.oecd$pc, re.oecd$country, geometric.mean)
## technical efficiency for each country
tc.c <- tapply(re.oecd$tc, re.oecd$country, geometric.mean)
## efficiency change for each country
ec.c <- tapply(re.oecd$ec, re.oecd$country, geometric.mean)
#missing time series 1992-2002 TURKEY, KOREA, LUXEMBOURG AND MEKSIKO capital stock data
#VUOSITTAINEN startyear-endyear KESKIARVO TEHOKKUUSKERTOIMESSA (MALMQUIST - FARREL)
#ec: efficiency change #TEHOKKUUSMUUTOS
ec.c_df <- as.data.frame(ec.c)
summary(ec.c_df)
ec.c_df
#tc: technical change #TEKNISEN TEHOKKUUDEN MUUTOS
tc.c_df <- as.data.frame(tc.c)
#pc: productivity change #TUOTTAVUUDEN MUUTOS
pc.c_df <- as.data.frame(pc.c)
#LITTLE TRICK
#ec: efficiency change #TEHOKKUUSMUUTOS
write.table(ec.c_df, file = "c:/data/ec.c_df.txt", sep = "\t", col.names = NA, qmethod = "double")
ec.c_df2 <- read.table("c:/data/ec.c_df.txt", header=TRUE, sep="\t", na.strings="NA", dec=".", strip.white=TRUE)
names(ec.c_df2)<- c("Country", "Effiency")
#tc: technical change #TEKNISEN TEHOKKUUDEN MUUTOS
write.table(tc.c_df, file = "c:/data/tc.c_df.txt", sep = "\t", col.names = NA, qmethod = "double")
tc.c_df2 <- read.table("c:/data/tc.c_df.txt", header=TRUE, sep="\t", na.strings="NA", dec=".", strip.white=TRUE)
names(tc.c_df2)<- c("Country", "Effiency")
#pc: productivity change #TUOTTAVUUDEN MUUTOS
write.table(pc.c_df, file = “c:/data/pc.c_df.txt”, sep = “\t”, col.names = NA, qmethod = “double”)
pc.c_df2 <- read.table(“c:/data/pc.c_df.txt”, header=TRUE, sep=”\t”, na.strings=”NA”, dec=”.”, strip.white=TRUE)
names(pc.c_df2)<- c(“Country”, “Effiency”)
#REMOVING NA-VALUES
ec.c_df2 <- ec.c_df2[!is.na(ec.c_df2$Effiency),]
tc.c_df2 <- tc.c_df2[!is.na(tc.c_df2$Effiency),]
pc.c_df2 <- pc.c_df2[!is.na(pc.c_df2$Effiency),]
summary(ec.c_df2)
#just cecking country names
ec.c_df2$Country
#replace some country name with new one…
ec.c_df3 <- gsub(“United States of America”, “United States”, ec.c_df2$Country)
ec.c_df3 <- gsub(“Germany, West”, “Germany”, ec.c_df3)
ec.c_df3 <- gsub(“Korea, Republic”, “South Korea”, ec.c_df3)
tc.c_df3 <- gsub(“United States of America”, “United States”, tc.c_df2$Country)
tc.c_df3 <- gsub(“Germany, West”, “Germany”, tc.c_df3)
tc.c_df3 <- gsub(“Korea, Republic”, “South Korea”, tc.c_df3)
pc.c_df3 <- gsub(“United States of America”, “United States”, pc.c_df2$Country)
pc.c_df3 <- gsub(“Germany, West”, “Germany”, pc.c_df3)
pc.c_df3 <- gsub(“Korea, Republic”, “South Korea”, pc.c_df3)
#as a dataframe MUUNNETAAN DATA FRAMEKSI
ec.c_df3 <- as.data.frame(ec.c_df3)
tc.c_df3 <- as.data.frame(tc.c_df3)
pc.c_df3 <- as.data.frame(pc.c_df3)
#check total number of rows KATSOTAAN RIVINUMEROINNIT MERGELLE
summary(ec.c_df2)
nrow(ec.c_df2)
nrow(ec.c_df3)
summary(tc.c_df2)
nrow(tc.c_df2)
nrow(tc.c_df3)
summary(pc.c_df2)
nrow(pc.c_df2)
nrow(pc.c_df3)
#used in time series
#1980-1990
#1990-2009
#giving row id ...NUMEROIDDAAN ID MERGEÄ VARTEN
ec.c_df2$id1=c(1:26)
ec.c_df3$id1=c(1:26)
tc.c_df2$id1=c(1:26)
tc.c_df3$id1=c(1:26)
pc.c_df2$id1=c(1:26)
pc.c_df3$id1=c(1:26)
#...and for time series
#1991-2002
#giving row id ...NUMEROIDDAAN ID MERGEÄ VARTEN
ec.c_df2$id1=c(1:22)
ec.c_df3$id1=c(1:22)
tc.c_df2$id1=c(1:22)
tc.c_df3$id1=c(1:22)
pc.c_df2$id1=c(1:22)
pc.c_df3$id1=c(1:22)
#merge data table and renamed country by id .....
ec.c_df4 <-merge(ec.c_df2, ec.c_df3, by.x="id1", by.y="id1", all = TRUE)
tc.c_df4 <-merge(tc.c_df2, tc.c_df3, by.x="id1", by.y="id1", all = TRUE)
pc.c_df4 <-merge(pc.c_df2, pc.c_df3, by.x="id1", by.y="id1", all = TRUE)
#check the data
head(ec.c_df4)
head(tc.c_df4)
head(pc.c_df4)
summary(ec.c_df4)
#selecting columns to the gvisGeoMapping .....
ec.c_df5 <- data.frame(ec.c_df4$ec.c_df3, ec.c_df4$Effiency )
tc.c_df5 <- data.frame(tc.c_df4$tc.c_df3, tc.c_df4$Effiency )
pc.c_df5 <- data.frame(pc.c_df4$pc.c_df3, pc.c_df4$Effiency )
#check the data
head(ec.c_df5)
head(tc.c_df5)
head(pc.c_df5)
summary(ec.c_df5)
summary(tc.c_df5)
summary(pc.c_df5)
#naming trick
names(ec.c_df5)<- c("Country", "Effiency change in OECD 1980-1990")
names(tc.c_df5)<- c("Country", "Technical Effiency change in OECD 1980-1990")
names(pc.c_df5)<- c("Country", "Productivity change in OECD 1980-1990")
#naming time series 1991-2009
names(ec.c_df5)<- c("Country", "Effiency change in OECD 1991-2009")
names(tc.c_df5)<- c("Country", "Technical Effiency change in OECD 1991-2009")
names(pc.c_df5)<- c("Country", "Productivity change in OECD 1991-2009")
#1991-2002
names(ec.c_df5)<- c("Country", "Effiency change in OECD 1991-2002")
names(tc.c_df5)<- c("Country", "Technical Effiency change in OECD 1991-2002")
names(pc.c_df5)<- c("Country", "Productivity change in OECD 1991-2002")
head(ec.c_df5)
head(tc.c_df5)
head(pc.c_df5)
#set library
library(googleVis)
#1980-1990
#me/230712
#1
#KMEAN VALUE OF MALMQUIST INDICES 1980-1990 Efficency change
Geo1=gvisGeoMap(ec.c_df5, locationvar="Country", numvar="Effiency change in OECD 1980-1990", options=list (height=450, width=800, dataMode='regions'))
#plot(Geo1)
cat(Geo1$html$chart, file=".../oecd_mean_eff_1980_1990_malmquist2.html")
#2
#KESKIARVO MEAN VALUE OF MALMQUIST INDICES 1980-1990 Efficency change
Geo2=gvisGeoMap(tc.c_df5, locationvar="Country", numvar="Technical Effiency change in OECD 1980-1990", options=list(height=450, width=800, dataMode='regions'))
#plot(Geo2)
cat(Geo2$html$chart, file=".../oecd_mean_tech_eff_1980_1990_malmquist2.html")
#3
#KESKIARVO MEAN VALUE OF MALMQUIST INDICES 1980-1990 Efficency change
Geo3=gvisGeoMap(pc.c_df5, locationvar="Country", numvar="Productivity change in OECD 1980-1990", options=list(height=450, width=800, dataMode='regions'))
#plot(Geo3)
cat(Geo3$html$chart, file=".../oecd_mean_prod_1980_1990_malmquist2.html")
#1991-2009 (capital var dropped)
#me/240712
#1
#KESKIARVO MEAN VALUE OF MALMQUIST INDICES
Geo1=gvisGeoMap(ec.c_df5, locationvar="Country", numvar="Effiency change in OECD 1991-2009", options=list (height=450, width=800, dataMode='regions'))
plot(Geo1)
cat(Geo1$html$chart, file=".../oecd_mean_eff_1991_2009_malmquist2.html")
#2
#VALUE OF MALMQUIST INDICES
Geo2=gvisGeoMap(tc.c_df5, locationvar="Country", numvar="Technical Effiency change in OECD 1991-2009", options=list(height=450, width=800, dataMode='regions'))
plot(Geo2)
cat(Geo2$html$chart, file=".../oecd_mean_tech_eff_1991_2009_malmquist2.html")
#3
#KESKIARVO MEAN VALUE OF MALMQUIST INDICES
Geo3=gvisGeoMap(pc.c_df5, locationvar="Country", numvar="Productivity change in OECD 1991-2009", options=list(height=450, width=800, dataMode='regions'))
plot(Geo3)
cat(Geo3$html$chart, file=".../oecd_mean_prod_1991_2009_malmquist2.html")
#1991-2002 (capital as input)
#me/240712
#1
#KESKIARVO MEAN VALUE OF MALMQUIST INDICES
Geo1=gvisGeoMap(ec.c_df5, locationvar="Country", numvar="Effiency change in OECD 1991-2002", options=list (height=450, width=800, dataMode='regions'))
plot(Geo1)
cat(Geo1$html$chart, file=".../oecd_mean_eff_1991_2002_malmquist2.html")
#2
#KESKIARVO MEAN VALUE OF MALMQUIST INDICES
Geo2=gvisGeoMap(tc.c_df5, locationvar="Country", numvar="Technical Effiency change in OECD 1991-2002", options=list(height=450, width=800, dataMode='regions'))
plot(Geo2)
cat(Geo2$html$chart, file=".../oecd_mean_tech_eff_1991_2002_malmquist2.html")
#3
#KESKIARVO MEAN VALUE OF MALMQUIST INDICES
Geo3=gvisGeoMap(pc.c_df5, locationvar="Country", numvar="Productivity change in OECD 1991-2002", options=list(height=450, width=800, dataMode='regions'))
plot(Geo3)
cat(Geo3$html$chart, file=".../oecd_mean_prod_1991_2002_malmquist2.html")
World Map (producitivity, efficiency)
1980-1990
oecd_mean_eff_1980_1990_malmquist2
oecd_mean_prod_1980_1990_malmquist2
oecd_mean_tech_eff_1980_1990_malmquist2
1991-2002
oecd_mean_eff_1991_2002_malmquist2
oecd_mean_prod_1991_2002_malmquist2
oecd_mean_tech_eff_1991_2002_malmquist2
1991-2009
oecd_mean_eff_1991_2009_malmquist2
oecd_mean_prod_1991_2009_malmquist2
oecd_mean_tech_eff_1991_2009_malmquist2
The cubic smoothing spline model
Now we plot productivity, effectiveness and technical effectiveness mean values historical trend and forecast by using
The cubic smoothing spline model. It is equivalent to an ARIMA(0,2,2) model.
###############################################################
library(forecast)
#library(ggplot2)
#1980-1990
#1990-2009
#1991-2002
#####################################################################
#1
#1980-1990
#####################################################################
#PRODUCTIVITY
pc.y
fcast_pc <- splinef(pc.y,h=10, fan=T) #NOTE confidence leve 50, 99
plot(fcast_pc, main="Productivity, forecast from Cubic Smoothing Spline", ylab="Malmquist indices - Productivity", xlab="Year(0=1980, 10=1990, 20=2000)")
# example – output graph to jpeg file
jpeg(“…/Productivity 1980_1990_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_pc, main=”Productivity, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Productivity”, xlab=”Year(0=1980, 10=1990, 20=2000)”)
dev.off()

#TECHNICAL EFFICIENCY
fcast_tc <- splinef(tc.y,h=10, fan=T)
plot(fcast_tc, main=”Technical Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Technical Efficiency”, xlab=”Year(0=1980, 10=1990, 20=2000)”)
# example – output graph to jpeg file
jpeg(“…/Technical efficiency 1980_1990_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_tc, main=”Technical Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Technical Efficiency”, xlab=”Year(0=1980, 10=1990, 20=2000)”)
dev.off()
#EFFICIENCY
fcast_ec <- splinef(ec.y,h=10, fan=T)
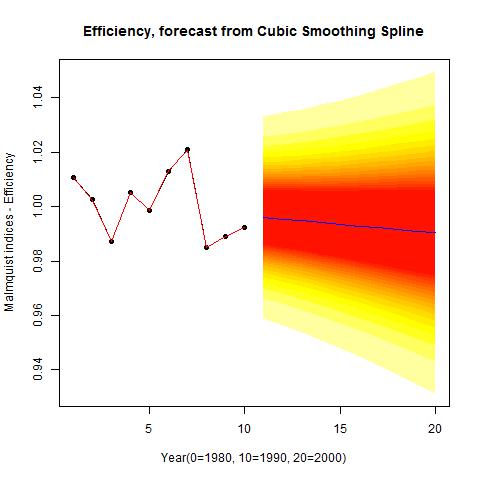
plot(fcast_ec, main=”Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Efficiency”, xlab=”Year(0=1980, 10=1990, 20=2000)”)
# example – output graph to jpeg file
jpeg(“G:/data/home/2012/marko/blogi_rbloggerqvist/tekstiaihiot/40/Efficiency 1980_1990_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_ec, main=”Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Efficiency”, xlab=”Year(0=1980, 10=1990, 20=2000)”)
dev.off()
summary(fcast_pc)
summary(fcast_tc)
summary(fcast_ec)
#####################################################################
#2
#1991-2009
#####################################################################
#PRODUCTIVITY
pc.y
fcast_pc <- splinef(pc.y,h=10, fan=T) #NOTE confidence leve 50, 99
plot(fcast_pc, main=”Productivity, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Productivity”, xlab=”Year(0=1990, 20=2010)”)
# example – output graph to jpeg file
jpeg(“…/Productivity 1991_2009_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_pc, main=”Productivity, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Productivity”, xlab=”Year(0=1990, 20=2010)”)
dev.off()
#TECHNICAL EFFICIENCY
fcast_tc <- splinef(tc.y,h=10, fan=T)
plot(fcast_tc, main=”Technical Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Technical Efficiency”, xlab=”Year(0=1990, 20=2010)”)
# example – output graph to jpeg file
jpeg(“G:/data/home/2012/marko/blogi_rbloggerqvist/tekstiaihiot/40/Technical efficiency 1991_2009_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_tc, main=”Technical Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Technical Efficiency”, xlab=”Year(0=1990, 20=2010)”)
dev.off()
#EFFICIENCY
fcast_ec <- splinef(ec.y,h=10, fan=T)
plot(fcast_ec, main=”Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Efficiency”, xlab=”Year(0=1990, 20=2010)”)
# example – output graph to jpeg file
jpeg(“…/Efficiency 1991_2009_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_ec, main=”Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Efficiency”, xlab=”Year(0=1990, 20=2010)”)
dev.off()
summary(fcast_pc)
summary(fcast_tc)
summary(fcast_ec)
######################################################################3
#1991-2002 (capital included)
#
#####################################################################
#PRODUCTIVITY
fcast_pc <- splinef(pc.y,h=10, fan=T) #NOTE confidence leve 50, 99
plot(fcast_pc, main=”Productivity, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Productivity”, xlab=”Year(1=1991, 10=2000, 20=2012)”)
# example – output graph to jpeg file
jpeg(“…/Productivity 1991_2002_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_pc, main=”Productivity, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Productivity”, xlab=”Year(1=1991, 10=2000, 20=2012)”)
dev.off()
#TECHNICAL EFFICIENCY
fcast_tc <- splinef(tc.y,h=10, fan=T)
plot(fcast_tc, main=”Technical Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Technical Efficiency”, xlab=”Year(1=1991, 10=2000, 20=2012)”)
# example – output graph to jpeg file
jpeg(“…/Technical efficiency 1991_2002_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_tc, main=”Technical Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Technical Efficiency”, xlab=”Year(1=1991, 10=2000, 20=2012)”)
dev.off()
#EFFICIENCY
fcast_ec <- splinef(ec.y,h=10, fan=T)
plot(fcast_ec, main=”Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Efficiency”, xlab=”Year(1=1991, 10=2000, 20=2012)”)
# example – output graph to jpeg file
jpeg(“…/Efficiency 1991_2002_Forecast Cubic_Smoothing_Spline10y2.jpg”)
plot(fcast_ec, main=”Efficiency, forecast from Cubic Smoothing Spline”, ylab=”Malmquist indices – Efficiency”, xlab=”Year(1=1991, 10=2000, 20=2012)”)
dev.off()
summary(fcast_pc)
summary(fcast_tc)
summary(fcast_ec)
#####################################################################
Ok, that’s it,
Have fun with Linear Programming for the Malmquist Productivity Growth Index and its wide range of applications…
Marko